Pulse sequence magnetization of single-excitation switching power supply transformer core part 2
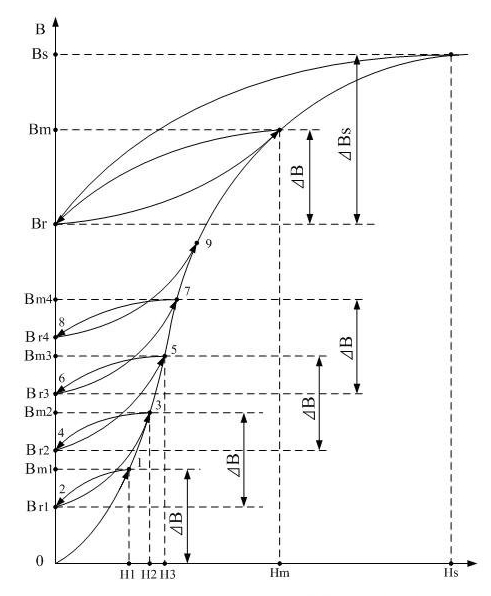
The magnetic field strength H drops to zero, but the magnetic flux density in the transformer core can not follow the magnetic field strength to zero, but can only drop to a residual value of magnetic flux density, this phenomenon is called the transformer core has magnetic coercivity, referred to as coercivity, expressed by Hc. Transformer core has magnetic coercivity, which is the most basic property of ferromagnetic materials or magnetic materials. Similarly, when the second DC pulse is added to both ends of the transformer primary coil a and B, the magnetic flux density B in the transformer core will rise according to the new magnetization curve 2-3 in Figure 2-2, and the magnetic flux density will be magnetized to the second maximum Bm2 by the magnetic field strength, resulting in an incremental ΔB, ΔB = BM2-br1.
After the end of the second DC pulse, the excitation current in the primary coil of the transformer drops to zero, and the back electromotive force generated by the primary and secondary coils of the transformer will return the magnetic flux density to the second residual magnetic flux density Br2 according to another new demagnetization curve 3-4. Of course, Br2 is also just another temporary residual value in the process of magnetic flux density change when the transformer core is demagnetized.
And so on, the third and fourth DC pulse voltages will also increase the magnetic flux density by an increment ΔB, that is:
ΔB = Bm3-Br2 = Bm4-Br3 = Bm1-0 (2-9)
In formula (2-9), ΔB is the increment of magnetic flux density; As long as the amplitude U and pulse width τ of the pulse voltage acting on the switching transformer coil are unchanged, the magnetization process of the transformer iron chip will be carried out under the condition that the flux density increment is constant (∆B = constant).
However, when the amplitude and width of the DC pulse are unchanged, the increment ΔB of the magnetic flux density does not change, which does not mean that the increment of the magnetic field strength can be guaranteed to remain unchanged, which is an important difference between the magnetic intensity and the magnetic field strength.
After n DC pulse voltages, the maximum magnetic flux density Bm and residual magnetic flux density Br in the transformer core can basically stabilize above a certain value, that is, after the pulse train reaches a stable state, the magnetization process will repeat along a fixed local hysteresis loop n point on the original curve. At this time, the residual magnetic flux density is Br n(Br n= Br), and the ΔB value of the magnetic flux density is basically unchanged regardless of the increase or decrease of the magnetic field intensity.
Obviously, where the local hysteresis loop is fixed for a particular material depends only on the magnitude of ∆B. If ∆B is large enough, the lowest point of the local hysteresis loop is at the residual flux density point Br of the maximum local hysteresis loop. At this time, Br corresponds to the starting point of each input DC pulse, and Bm corresponds to the end point of each DC pulse.
It is understandable that the magnetic flux density does not continue to increase after reaching the maximum Bm, because the magnetic flux density and magnetic field intensity can be either potential energy or potential energy, and the two can be converted into each other, and they are very similar to the process of capacitor charge and discharge.
For example, when the power supply voltage charges the capacitor, the voltage at both ends of the capacitor will rise; When the power supply is disconnected, the capacitor will discharge to the load, and the voltage at both ends will drop; When the charge of the capacitor is exactly equal to the charge of the discharge, the voltage ripple at both ends of the capacitor will stabilize above a certain value.
The magnetic field strength increment is represented by ∆H, which corresponds to the magnetic flux density increment ∆B on the fixed local hysteresis loop, that is, the following relationship can be expressed between them:
ΔB = f(∆H) (2-10)
Formula (2-10) is called the pulse static characteristic relationship between magnetic field intensity increment ∆H and magnetic flux density increment ∆B. Under the condition of DC state, equation (2-10) is not valid.
The corresponding relationship between the magnetic field intensity increment ∆H and the magnetic flux density increment ∆B can also be expressed as follows:
μ△=ΔB/∆H — Pulse transformer (2-11)
In the formula (2-11), μ△ is called the pulse static magnetization coefficient, or the pulse permeability of the pulse transformer. Because the use of pulse permeability is relatively small, we can also use the concept of average permeability μa for switching transformers. To wit:
μa=ΔBa/∆Ha — Switching transformer (2-12)
In formula (2-12), μa is the average magnetic permeability of the switching transformer; ΔBa is the average flux density increment in the core of the switching transformer. ∆Ha is the average magnetic field strength increment in the switching transformer core.
The difference between the pulse permeability μ△ and the average permeability μa is that the amplitude and width of the input pulse voltage of the general pulse transformer are basically fixed, and it is a unipolar pulse, and the area of the hysteresis loop is relatively small, therefore, the pulse permeability μ△ of the iron core can almost be regarded as a constant; The amplitude and width of the input pulse voltage of the switching transformer are not fixed, the area of the hysteresis loop is relatively large, and the change range of the magnetic permeability of the core is also large, especially the double-excited switching transformer, so it can only be described by the concept of average magnetic permeability μa.
When the excitation current or magnetic field strength magnetizes the transformer core, it also has characteristics similar to that of capacitor charge and discharge: When the magnetic field strength generated by the excitation current in the transformer primary coil magnetizes the transformer core, the magnetic flux density will increase, which is equivalent to charging the capacitor; When the excitation current in the primary coil of the transformer is zero, the primary and secondary coils of the transformer will generate a back electromotive force, and the current generated by the induction will generate a reverse magnetic field to demagnetize the transformer core, so that the magnetic flux density decreases, which is similar to the discharge of the charging capacitor to the load.
When the flux density increment generated when the transformer core is magnetized is exactly equal to the flux density increment (negative value) generated when the transformer core is demagnetized, the maximum flux density Bm and the residual flux density Br in the transformer core will stabilize above a certain value respectively.
At this time, we can say that the magnetization process of the transformer core has entered a basically stable state, that is, each input DC pulse voltage, the magnetic flux density in the transformer core will produce a magnetic flux density increment ΔB, ΔB = BM-br, when the DC pulse is over, the magnetic flux density returns from the maximum Bm to the position of the residual magnetic flux density Br. In this way, the Br value corresponding to the magnetization curve is called the remanent magnetic (or residual magnetic flux density), and the Bm value corresponding to the magnetization curve is called the maximum magnetic flux density.
However, the values of the maximum magnetic flux density Bm and the residual magnetic flux density Br in the magnetization curve of the transformer core are not invariable, and they will change with the amplitude of the input pulse voltage and the pulse width. Only when the amplitude and pulse width of the input pulse voltage remain basically unchanged, the values of the maximum magnetic flux density Bm and the residual magnetic flux density Br in the magnetization curve of the transformer core will remain basically unchanged.
As for how many DC pulse voltages to go through, the magnetic flux density in the core of the switching transformer reaches the maximum Bm, which is related to the amplitude of the DC pulse voltage, and is also related to the pulse width of the DC pulse voltage, that is, the volt-second capacity of the switching transformer. The larger the volt-second capacity of the switching transformer, the smaller the value of the flux density increment ΔB generated by each DC pulse, so the more DC pulses are needed. Conversely, the smaller the volt-second capacity of the transformer, the fewer DC pulses are required. When the volt-second capacity of the transformer is very small, only one DC pulse may be needed to reach the maximum magnetic flux density Bm, and even make the transformer core magnetic saturation.
The volt-second capacity of the transformer has a great influence on the magnetization curve. The larger the volt-second capacity of the transformer, the smaller the flux density increment ΔB corresponding to each DC pulse voltage, and the smaller the maximum flux density Bm. For the same transformer core material, the corresponding Bm value and Br value are also different if the volt-second capacity of the transformer is selected. Therefore, the volt-second capacity of a transformer is a very important parameter for transformer design.
If the volt-second capacity of the transformer is relatively small, and the DC pulse voltage amplitude added to both ends of the transformer primary coil a and b is relatively high, and the pulse width is relatively wide, the excitation current flowing through the transformer primary coil will be large; At this time, the magnetic flux density in the transformer core will be easily saturated. When the magnetic flux density in the transformer core is saturated, the magnetic flux density B or the magnetic flux will not increase with the increase of the magnetic field strength or excitation current, at this time the maximum magnetic flux density is generally called the saturated magnetic flux density, expressed by Bs, and the corresponding magnetic flux density increment is expressed by ΔBs.
It is also necessary to add that the process of magnetization and demagnetization of the transformer core is very similar to the process of charging and discharging of capacitors, but there is still a big difference. After the capacitor is fully charged, if the power supply is disconnected and the capacitor is no longer charged, the capacitor will discharge the load, and the discharge process will continue until all the charges stored in the capacitor release light; After the transformer core is magnetized to the maximum magnetic flux density Bm, the back electromotive force generated by the primary and secondary coils of the transformer and the reverse magnetic field generated by its induced current demagnetize the transformer core, but the magnetic flux density cannot be returned from the maximum Bm to zero, but can only be returned to the residual magnetic flux density Br.
When the magnetic field strength H drops to zero, the magnetic flux density in the transformer core cannot follow back to zero, but can only return to the residual magnetic flux density Br. This phenomenon is called the magnetic coercivity of the transformer core, referred to as coercivity, expressed by Hc; This also shows that the magnetization process of the transformer core is irreversible. There is magnetic coercivity in the transformer core, which is the most basic property of ferromagnetic materials or magnetic materials; Magnetic materials with different properties have different magnetic coercivity. Generally, transformer iron cores are made of ferromagnetic materials with small magnetic coercivity.
The concept of magnetic coercivity Hc of transformer core is different from that of the residual magnetic flux density Br. From the definition of magnetic coercivity, the magnetic coercivity Hc is that when the transformer core is demagnetized, the maximum residual magnetic flux density Brm decreases to 0, corresponding to the required magnetic field strength. However, the maximum residual magnetic flux density Brm here refers to the residual magnetic flux density Br generated when the transformer core reaches magnetic saturation, because the general residual magnetic flux density Br is corresponding to the dynamic maximum magnetic flux density.
But we do not understand that only after the transformer core reaches magnetic saturation, there will be magnetic coercivity; In the process of magnetizing the transformer core, the magnetic coercivity exists from beginning to end, but it is not the same as the conventionally defined Hc in value. Magnetic coercivity, like magnetic permeability, is also used to cover up the concept of the intrinsic relationship between magnetic field strength and electromagnetic flux density that has not yet been fully revealed by humans.
Therefore, strictly speaking, the magnetic coercivity also changes with the size of the magnetic field strength H, which is the same as the magnetic flux density, and tends to saturation with the increase of the magnetic field strength H. This is the main reason why the maximum magnetic flux density Bm and the residual magnetic flux density Br in the transformer core can finally stabilize above a certain value, respectively.
Figure 2-2
As can be seen from Figure 2-2, with the increase of magnetic flux density, the magnetic field strength needs to increase more, because the magnetic permeability of the iron core will become smaller with the increase of the magnetic field strength, and the magnetic coercivity of the iron core will not increase with the increase of the magnetic field strength, and it will always have a limit value. When the reverse electromotive force and induced current are generated in the transformer coil, and the reverse magnetic field generated by the induced current demagnetize the transformer core, the increment of the magnetic permeability and magnetic coercivity of the core will change in the direction of increase. Therefore, for each input pulse voltage, a dynamic balance point can always be found between the magnetic flux density, magnetic field strength and magnetic coercivity. The maximum magnetic flux density Bm and the residual magnetic flux density Br in the transformer core can be relatively stable.
Post time: Nov-29-2024